Senmotic ist deswegen so wirkungsvoll, weil wir an den Faszien arbeiten.

Was sind nun aber diese Faszien? Dazu erfahren Sie im Folgenden alles Wissenswerte in Text, Bild und Ton. Faszien tauchen mittlerweile auch als Trendthema in den Medien auf. Quarks & Co - die Wissenschaftssendung mit Ranga Yogeshar widmet sich intensiv dem Thema "Faszien" und ermöglicht erstaunliche Einblicke in die Welt der faszialen Bindegewebe. Die Sendung demonstriert, warum auch für Rückenschmerzen häufig die Faszien verantwortlich sind.

Faszien - kompakt und verständlich

Faszien sind feine, zähe bindegewebige Häute. Fast jeder hat schon einmal Fasziengewebe gesehen. Wer schon einmal eine Hühnerbrust geschnitten hat, dem ist vielleicht die weiße, fasrige Hülle aufgefallen, die das Fleisch umhüllt. Das ist Faszie! Genau wie der Körper des Tieres, wird auch der menschliche Körper von diesem Gewebe umhüllt und durchzogen. Die menschlichen Faszien umhüllen ausnahmslos jeden Muskel, jeden Knochen, die Organe und selbst die Nerven wie eine Art Bonbonpapier. Diese Hüllen haben keinen Anfang und kein Ende und ziehen sich nahtlos ineinander übergehend, von Kopf bis Fuß durch den Körper.

Durch psychischen Stress, Operationen, Schonhaltungen, Verspannungen, Bewegungsmangel und Haltungsfehler können Faszien verhärten, sich verkürzen und intensiv miteinander verkleben (Prof. Dr. med. Paulini, Universitäten Ulm und Mainz). Auf Grund dessen verlieren sie ihre Gleitfähigkeit und grenzen den Bewegungsspielraum unserer Muskulatur und unserer Gelenke dauerhaft ein. Bewegungseinschränkungen, Schmerzen und die typischen Haltungsfehler sind die Folge. Der Körper verliert seine Mitte und die Schwerkraft drückt ihn nieder.

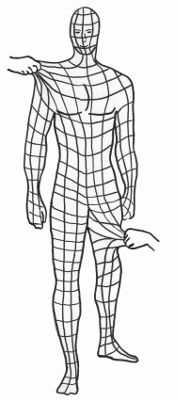
Dazu kommt, dass alle Faszien untereinander in Verbindung stehen und Spannungen sowie Unbeweglichkeiten in andere Körperteile übertragen. Sie können sich das am einfachsten folgendermaßen vorstellen:

Greifen sie einmal beherzt ihr Oberteil mit einer Hand. Ihre Finger greifen sich den Stoff und Sie drehen die Hand so weit sie können im oder gegen den Uhrzeiger. Sie werden bemerken, dass das Oberteil Falten wirft, die alle in Richtung Ihrer Hand zeigen. Sie werden bemerken, wie der Kragen des Oberteils sich jetzt deutlicher an den Hals schnürt und es auch um die Brust etwas enger wird. Sie werden auch bemerken, dass Sie sich noch immer frei bewegen können, aber einfacher wird es sein, sich zu der den Stoff festhaltenden Hand hinzubewegen, als von ihr weg.

Ähnlich können Sie sich die Beweglichkeit Ihres Körpers vorstellen, wenn Verklebungen oder Verkürzungen von Faszien vorliegen. Nur handelt es sich dann nicht nur um ein Oberteil, sondern um eine Art Ganzkörperanzug, der den kompletten Körper umspannt und auch durchzieht, da dieses Gewebe eben keinen Anfang und kein Ende hat. Stellen Sie sich einen Overall oder Ballettanzug vor, das trifft es ganz gut. Zieht jemand hier z.B. auf Höhe des Beins kräftig an so einem Anzug, wird die Spannung und der Zug für den Träger selbst bis zum Nacken spürbar sein.

Deshalb kann z.B. eine verkürzte oder verklebte Wadenfaszie über die Beine einen Zug auf unseren unteren Rücken, oder sogar die Schulter und den Kopf ausüben und dort für Bewegungseinschränkungen, Schmerzen und Unbehagen sorgen. So sehr uns das zum Nachteil gereicht, so sehr können wir auch davon profitieren. Denn mobilisiere ich nur eine einzige Faszie in dieser Kette, erreiche ich sehr viele Faszien vom Kopf bis zur Fußspitze. Senmotic Faszien-Therapie löst verklebte Faszien von Kopf bis Fuß, in 10 ausgeklügelt, aufeinander abgestimmten Sitzungen und bringt Sie so wieder in Form.

Interesse geweckt? Noch etwas mehr über Faszien, erfahren Sie in 10 sehr interessanten Punkten hier.